Fractale du mot de Fibonacci

La fractale du mot de Fibonacci est une courbe plane fractale définie à partir du mot de Fibonacci.

Définition

Cette courbe se construit itérativement en appliquant au mot de Fibonacci : 0100101001001... la règle OEDR (Odd-Even Drawing Rule). Pour chaque chiffre en position k :

• si le chiffre est 1 : tracer un segment de longueur 1 dans la direction précédente
• si le chiffre est 0, tracer un segment de longueur 1 après avoir fait un quart de tour:
  • à droite si k est pair
  • à gauche si k est impair

À un mot de Fibonacci de longueur ${\displaystyle F_{n}}$ où ${\displaystyle F_{n}}$ est le n-ième nombre de Fibonacci, est donc associée une courbe formée de ${\displaystyle F_{n}}$ segments. La courbe se présente sous trois aspects différents suivant que n est de la forme 3k, 3k 1, ou 3k 2.

Propriétés

Propriétés.

• La courbe ${\displaystyle {\mathcal {F}}_{n}}$, à ${\displaystyle F_{n}}$ segments, présente ${\displaystyle F_{n-1}}$ angles droits et ${\displaystyle F_{n-2}}$ angles plats.
• La courbe ne présente jamais d'auto-intersection, ni de points doubles. À la limite, elle présente une infinité de points asymptotiquement proches.
• La courbe présente des autosimilarités à toutes les échelles. Le facteur de réduction vaut ${\displaystyle 1 {\sqrt {2}}}$. Ce nombre, appelé également nombre d'argent ${\displaystyle \delta _{Ag}=\varphi _{2}}$, est présent dans nombre des propriétés géométriques évoquées ci-dessous.
• Le nombre de copies autosimilaires au degré n est un nombre de Fibonacci moins 1 (plus précisément : ${\displaystyle F_{3n 3}-1}$).
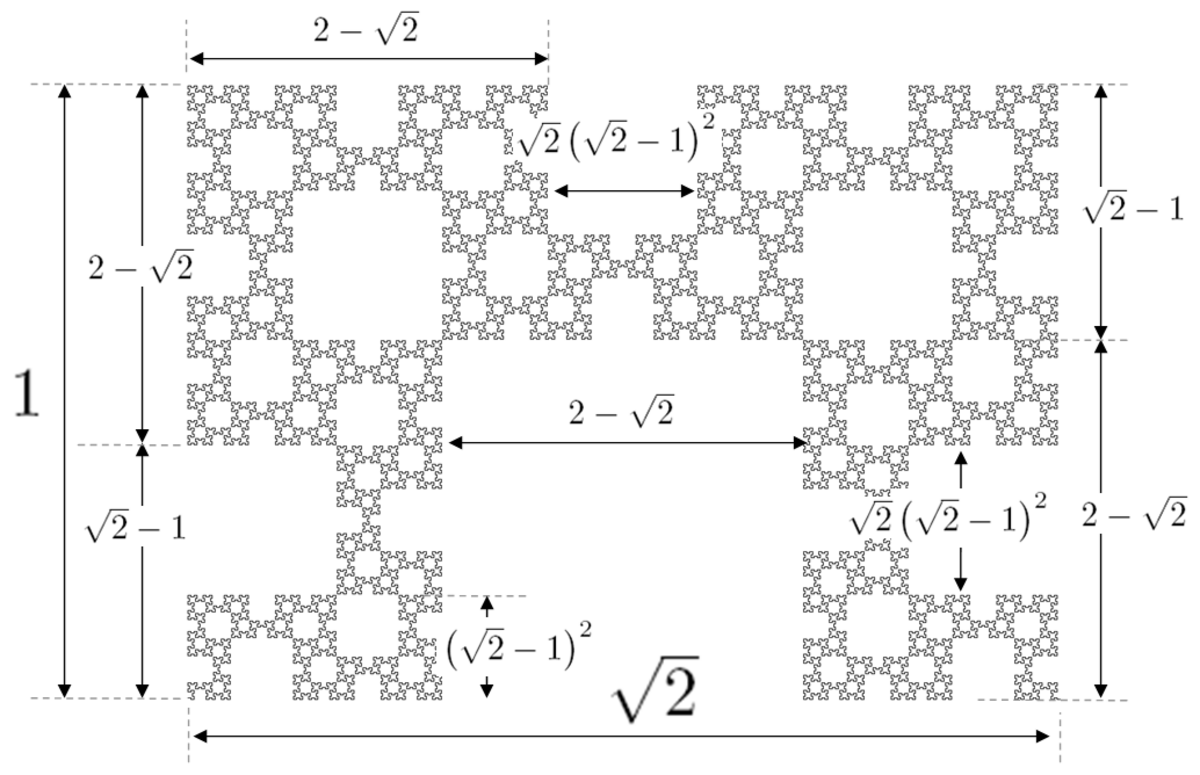
• La courbe délimite une infinité de structures carrées de taille décroissante, dans un rapport de ${\displaystyle 1 {\sqrt {2}}}$.
• Ce nombre de carrés est un nombre de Fibonacci.
• La courbe peut également être construite de diverses manières (voir galerie) :
  • système de fonctions itérées à 4 et 1 homothéties de rapport ${\displaystyle 1/\left(1 {\sqrt {2}}\right)}$ et ${\displaystyle 1/\left(1 {\sqrt {2}}\right)^{2}}$ ;
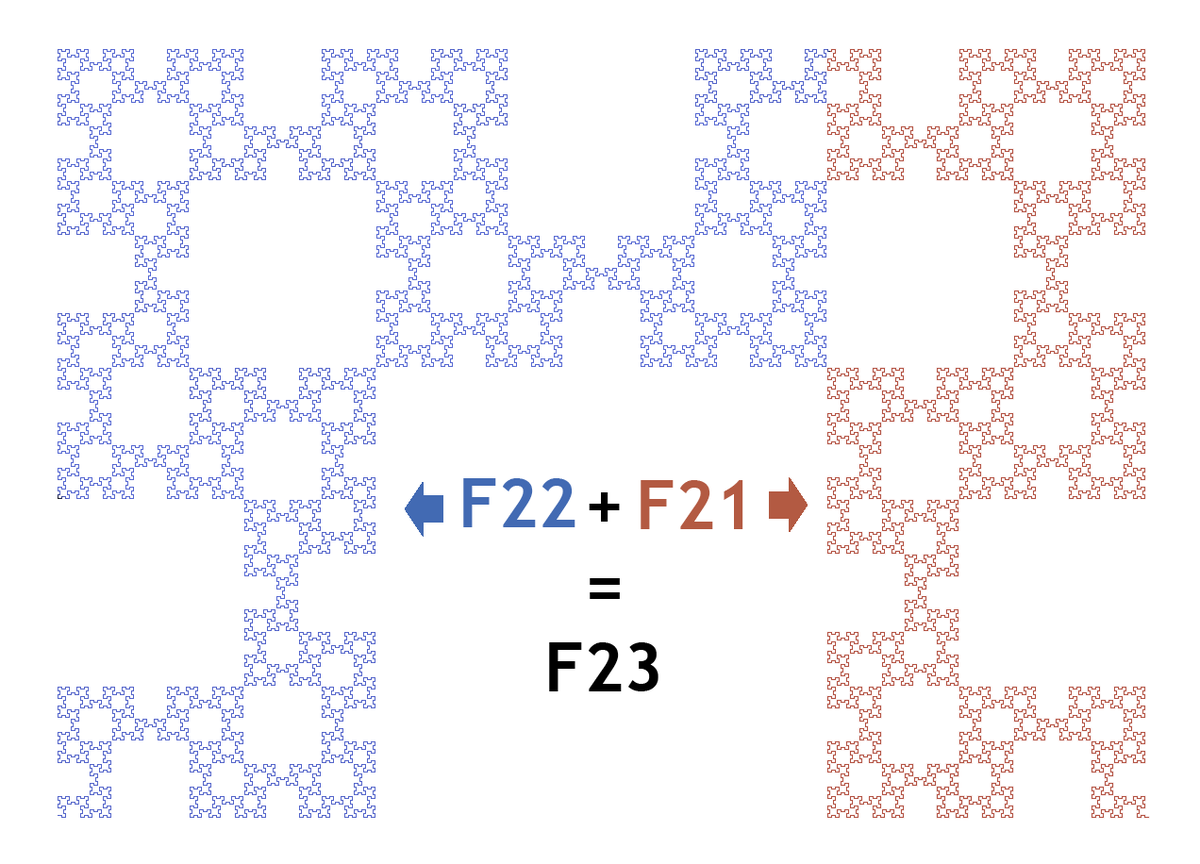
  • juxtaposition des courbes n – 1 et n – 2 ;
  • système de Lindermayer ;
  • construction itérée de 8 motifs carrés autour de chaque motif carré ;
  • construction itérée d'octogones.
• La dimension de Hausdorff de la courbe vaut ${\displaystyle {\frac {3\log \varphi }{\log \left(1 {\sqrt {2}}\right)}}\approx 1{,}6379}$, avec ${\displaystyle \varphi ={\frac {1 {\sqrt {5}}}{2}}}$, le nombre d'or.
• En généralisant à un angle ${\displaystyle \alpha }$ quelconque entre 0 et ${\displaystyle \pi /2}$, sa dimension de Hausdorff vaut ${\displaystyle {\frac {3\log \varphi }{\log \left(1 a {\sqrt {(1 a)^{2} 1}}\right)}}}$, avec ${\displaystyle a=\cos \alpha }$.
• La dimension de Hausdorff de sa frontière vaut ${\displaystyle {\frac {\log 3}{\log \left(1 {\sqrt {2}}\right)}}\approx 1{,}2465}$.
• Interchanger le rôle de "0" et de "1" dans le mot de Fibonacci, ou dans la règle, génère la même courbe, mais orientée à 45°.
• À partir du mot de Fibonacci, on peut définir le « mot dense de Fibonacci », sur un alphabet de 3 lettres : 102210221102110211022102211021102110221022102211021... (suite A143667 de l'OEIS). L'application, sur ce mot, d'une règle de traçage « naturelle » permet de définir un ensemble infini de variantes de la courbe, parmi lesquelles :
  • la variante « diagonale » ;
  • la variante « svastika » ;
  • la variante « compacte ».
• On conjecture que le motif de la fractale du mot de Fibonacci se retrouve pour tout mot sturmien dont la séquence directive (donc expansion de la pente en fractions continues) se termine par une suite infinie de "1".

Galerie

Tuile de Fibonacci

La juxtaposition de 4 courbes de Fibonacci de type ${\displaystyle F_{3k}}$ permet la construction d'une courbe fermée délimitant une surface connexe d'aire non nulle. Cette figure est appelée "tuile de Fibonacci".

• La tuile de Fibonacci pave presque le plan. La juxtaposition de 4 tuiles (voir illustration) laisse au centre un carré libre dont la surface tend vers zéro à mesure que k tend vers l'infini. À la limite, la tuile de Fibonacci pave le plan.
• Si la tuile de Fibonacci s'inscrit dans un carré de côté 1, alors son aire tend vers ${\displaystyle 2-{\sqrt {2}}\approx 0{,}5857}$.

Flocon de Fibonacci

Le flocon de Fibonacci est une tuile de Fibonacci définie selon la règle suivante :

• ${\displaystyle q_{n}=q_{n-1}q_{n-2}}$ si ${\displaystyle n\equiv 2{\pmod {3}}}$ ;
• ${\displaystyle q_{n}=q_{n-1}{\overline {q_{n-2}}}}$ sinon.

Avec ${\displaystyle q_{0}=\epsilon }$ et ${\displaystyle q_{1}=D}$, ${\displaystyle G=}$"tourne à gauche" et ${\displaystyle D=}$"tourne à droite", et ${\displaystyle {\overline {D}}=G}$,

Quelques propriétés remarquables^, :

• C'est la tuile de Fibonacci associée à la variante "diagonale" définie précédemment.
• Il pave le plan à toute itération (à tout ordre)
• Il pave le plan par translation de deux façons différentes, il s'agit donc d'un double pseudo-carré.
• son périmètre, à l'ordre ${\displaystyle n}$, vaut ${\displaystyle 4F_{3n 1}}$.
• son aire, à l'ordre ${\displaystyle n}$, suit les index successifs de rang impair de la suite de Pell (définie par ${\displaystyle P_{0}=0}$, ${\displaystyle P_{1}=1}$ et ${\displaystyle P_{n}=2P_{n-1} P_{n-2}}$).

Notes et références

Voir aussi

Article connexe

Liste de fractales par dimension de Hausdorff

Lien externe

(en) S. Brlek, Combinatorial aspects of double squares, juillet 2009 (support de conférence, avec A. Blondin-Massé et S. Labbé)

• Portail de la géométrie